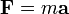The great question that has never been answered, and which I have not yet been able to answer, despite my thirty years of research into the feminine soul, is 'What does a woman want?'"
"Self-belief does not necessarily ensure success, but self-disbelief assuredly spawns failure."
"Common sense and a sense of humor are the same thing, moving at different speeds. A sense of humor is just common sense, dancing."
GREAT ENGINEER
JST FEEL IT
Thursday 5 April 2012
Tuesday 31 January 2012
my dream course
MECHANICS by prof jacob Jump to: navigation, search
This article is about an area of scientific study. For other uses, see Mechanic (disambiguation).
| | This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. (May 2010) |
Contents[hide] |
[edit] Classical versus quantum
| Quantum mechanics |
|---|
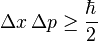 |
| Introduction Glossary · History |
| Fundamental concepts[show] |
| Formulations[show] |
| Equations[show] |
| Scientists[show] Bell · Bohm · Bohr · Born · Bose de Broglie · Dirac · Ehrenfest Everett · Feynman · Heisenberg Jordan · Kramers · von Neumann Pauli · Planck · Schrödinger Sommerfeld · Wien · Wigner |
Historically, classical mechanics came first, while quantum mechanics is a comparatively recent invention. Classical mechanics originated with Isaac Newton's laws of motion in Principia Mathematica, while quantum mechanics didn't appear until 1900. Both are commonly held to constitute the most certain knowledge that exists about physical nature. Classical mechanics has especially often been viewed as a model for other so-called exact sciences. Essential in this respect is the relentless use of mathematics in theories, as well as the decisive role played by experiment in generating and testing them.
Quantum mechanics is of a wider scope, as it encompasses classical mechanics as a sub-discipline which applies under certain restricted circumstances. According to the correspondence principle, there is no contradiction or conflict between the two subjects, each simply pertains to specific situations. The correspondence principle states that the behavior of systems described by quantum theories reproduces classical physics in the limit of large quantum numbers. Quantum mechanics has superseded classical mechanics at the foundational level and is indispensable for the explanation and prediction of processes at molecular and (sub)atomic level. However, for macroscopic processes classical mechanics is able to solve problems which are unmanageably difficult in quantum mechanics and hence remains useful and well used. Modern descriptions of such behavior begin with a careful definition of such quantities as displacement (distance moved), time, velocity, acceleration, mass, and force. Until about 400 years ago, however, motion was explained from a very different point of view. For example, following the ideas of Greek philosopher and scientist Aristotle, scientists reasoned that a cannonball falls down because its natural position is in the earth; the sun, the moon, and the stars travel in circles around the earth because it is the nature of heavenly objects to travel in perfect circles.
The Italian physicist and astronomer Galileo brought together the ideas of other great thinkers of his time and began to analyze motion in terms of distance traveled from some starting position and the time that it took. He showed that the speed of falling objects increases steadily during the time of their fall. This acceleration is the same for heavy objects as for light ones, provided air friction (air resistance) is discounted. The English mathematician and physicist Isaac Newton improved this analysis by defining force and mass and relating these to acceleration. For objects traveling at speeds close to the speed of light, Newton’s laws were superseded by Albert Einstein’s theory of relativity. For atomic and subatomic particles, Newton’s laws were superseded by quantum theory. For everyday phenomena, however, Newton’s three laws of motion remain the cornerstone of dynamics, which is the study of what causes motion.
[edit] Relativistic versus Newtonian
Analogous to the quantum versus classical reformation, Einstein's general and special theories of relativity have expanded the scope of mechanics beyond the mechanics of Newton and Galileo, and made fundamental corrections to them, that become significant and even dominant as speeds of material objects approach the speed of light, which cannot be exceeded.For example,
In Newtonian mechanics, Newton's laws of motion,
F=ma
whereas in Relativistic mechanics and Lorentz transformations, which were first discovered by Hendrik Lorentz,
F=γma
where γ is the Lorentz factor
[edit] General relativistic versus quantum
Relativistic corrections are also needed for quantum mechanics, although general relativity has not been integrated. The two theories remain incompatible, a hurdle which must be overcome in developing a theory of everything.[edit] History
Main articles: History of classical mechanics and History of quantum mechanics
| This section requires expansion. |
[edit] Antiquity
Main article: Aristotelian mechanics
The main theory of mechanics in antiquity was Aristotelian mechanics.[1] A later developer in this tradition was Hipparchus.[2][edit] Medieval age
Main article: Theory of impetus
In the Middle Ages, Aristotle's theories were criticized and modified by a number of figures, beginning with John Philoponus in the 6th century. A central problem was that of projectile motion, which was discussed by Hipparchus and Philoponus. This led to the development of the theory of impetus by 14th century French Jean Buridan, which developed into the modern theories of inertia, velocity, acceleration and momentum. This work and others was developed in 14th century England by the Oxford Calculators such as Thomas Bradwardine, who studied and formulated various laws regarding falling bodies.On the question of a body subject to a constant (uniform) force, the 12th century Jewish-Arab Nathanel (Iraqi, of Baghdad) stated that constant force imparts constant acceleration, while the main properties are uniformly accelerated motion (as of falling bodies) was worked out by the 14th century Oxford Calculators.
[edit] Early modern age
Two central figures in the early modern age are Galileo Galilei and Isaac Newton. Galileo's final statement of his mechanics, particularly of falling bodies, is his Two New Sciences (1638). Newton's 1687 Philosophiæ Naturalis Principia Mathematica provided a detailed mathematical account of mechanics, using the newly developed mathematics of calculus and providing the basis of Newtonian mechanics.[2]There is some dispute over priority of various ideas: Newton's Principia is certainly the seminal work and has been tremendously influential, and the systematic mathematics therein did not and could not have been stated earlier because calculus had not been developed. However, many of the ideas, particularly as pertain to inertia (impetus) and falling bodies had been developed and stated by earlier researchers, both the then-recent Galileo and the less-known medieval predecessors. Precise credit is at times difficult or contentious because scientific language and standards of proof changed, so whether medieval statements are equivalent to modern statements or sufficient proof, or instead similar to modern statements and hypotheses is often debatable.
[edit] Modern age
Two main modern developments in mechanics are general relativity of Einstein, and quantum mechanics, both developed in the 20th century based in part on earlier 19th century ideas.[edit] Types of mechanical bodies
Thus the often-used term body needs to stand for a wide assortment of objects, including particles, projectiles, spacecraft, stars, parts of machinery, parts of solids, parts of fluids (gases and liquids), etc.Other distinctions between the various sub-disciplines of mechanics, concern the nature of the bodies being described. Particles are bodies with little (known) internal structure, treated as mathematical points in classical mechanics. Rigid bodies have size and shape, but retain a simplicity close to that of the particle, adding just a few so-called degrees of freedom, such as orientation in space.
Otherwise, bodies may be semi-rigid, i.e. elastic, or non-rigid, i.e. fluid. These subjects have both classical and quantum divisions of study.
For instance, the motion of a spacecraft, regarding its orbit and attitude (rotation), is described by the relativistic theory of classical mechanics, while the analogous movements of an atomic nucleus are described by quantum mechanics.
[edit] Sub-disciplines in mechanics
The following are two lists of various subjects that are studied in mechanics.Note that there is also the "theory of fields" which constitutes a separate discipline in physics, formally treated as distinct from mechanics, whether classical fields or quantum fields. But in actual practice, subjects belonging to mechanics and fields are closely interwoven. Thus, for instance, forces that act on particles are frequently derived from fields (electromagnetic or gravitational), and particles generate fields by acting as sources. In fact, in quantum mechanics, particles themselves are fields, as described theoretically by the wave function.
[edit] Classical mechanics
- Newtonian mechanics, the original theory of motion (kinematics) and forces (dynamics)
- Hamiltonian mechanics, a theoretical formalism, based on the principle of conservation of energy
- Lagrangian mechanics, another theoretical formalism, based on the principle of the least action
- Celestial mechanics, the motion of bodies in space: planets, comets, stars, galaxies, etc.
- Astrodynamics, spacecraft navigation, etc.
- Solid mechanics, elasticity, the properties of deformable bodies.
- Fracture mechanics
- Acoustics, sound ( = density variation propagation) in solids, fluids and gases.
- Statics, semi-rigid bodies in mechanical equilibrium
- Fluid mechanics, the motion of fluids
- Soil mechanics, mechanical behavior of soils
- Continuum mechanics, mechanics of continua (both solid and fluid)
- Hydraulics, mechanical properties of liquids
- Fluid statics, liquids in equilibrium
- Applied mechanics, or Engineering mechanics
- Biomechanics, solids, fluids, etc. in biology
- Biophysics, physical processes in living organisms
- Statistical mechanics, assemblies of particles too large to be described in a deterministic way
- Relativistic or Einsteinian mechanics, universal gravitation
[edit] Quantum mechanics
The following are categorized as being part of Quantum mechanics:- Particle physics, the motion, structure, and reactions of particles
- Nuclear physics, the motion, structure, and reactions of nuclei
- Condensed matter physics, quantum gases, solids, liquids, etc.
- Quantum statistical mechanics, large assemblies of particles
[edit] Professional organizations
- Applied Mechanics Division, American Society of Mechanical Engineers
- Fluid Dynamics Division, American Physical Society
- Institution of Mechanical Engineers is the United Kingdom's qualifying body for Mechanical Engineers and has been the home of Mechanical Engineers for over 150 years.
- International Union of Theoretical and Applied Mechanics
history of mathematics
HISTORY OF MATHEMATICS
BY PROF JACOB
The area of study known as the history of mathematics is primarily an investigation into the origin of discoveries in mathematics and, to a lesser extent, an investigation into the mathematical methods and notation of the past.
Before the modern age and the worldwide spread of knowledge, written examples of new mathematical developments have come to light only in a few locales. The most ancient mathematical texts available are Plimpton 322 (Babylonian mathematics c. 1900 BC),[2] the Rhind Mathematical Papyrus (Egyptian mathematics c. 2000-1800 BC)[3] and the Moscow Mathematical Papyrus (Egyptian mathematics c. 1890 BC). All of these texts concern the so-called Pythagorean theorem, which seems to be the most ancient and widespread mathematical development after basic arithmetic and geometry.
The study of mathematics as a subject in its own right begins in the 6th century BC with the Pythagoreans, who coined the term "mathematics" from the ancient Greek μάθημα (mathema), meaning "subject of instruction".[4] Greek mathematics greatly refined the methods (especially through the introduction of deductive reasoning and mathematical rigor in proofs) and expanded the subject matter of mathematics.[5] Chinese mathematics made early contributions, including a place value system.[6][7] The Hindu-Arabic numeral system and the rules for the use of its operations, in use throughout the world today, likely evolved over the course of the first millennium AD in India and was transmitted to the west via Islamic mathematics.[8][9] Islamic mathematics, in turn, developed and expanded the mathematics known to these civilizations.[10] Many Greek and Arabic texts on mathematics were then translated into Latin, which led to further development of mathematics in medieval Europe.
From ancient times through the Middle Ages, bursts of mathematical creativity were often followed by centuries of stagnation. Beginning in Renaissance Italy in the 16th century, new mathematical developments, interacting with new scientific discoveries, were made at an increasing pace that continues through the present day.
The oldest known possibly mathematical object is the Lebombo bone, discovered in the Lebombo mountains of Swaziland and dated to approximately 35,000 BC.[12] It consists of 29 distinct notches cut into a baboon's fibula.[13] Also prehistoric artifacts discovered in Africa and France, dated between 35,000 and 20,000 years old,[14] suggest early attempts to quantify time.[15]
The Ishango bone, found near the headwaters of the Nile river (northeastern Congo), may be as much as 20,000 years old and consists of a series of tally marks carved in three columns running the length of the bone. Common interpretations are that the Ishango bone shows either the earliest known demonstration of sequences of prime numbers[13] or a six month lunar calendar.[16] In the book How Mathematics Happened: The First 50,000 Years, Peter Rudman argues that the development of the concept of prime numbers could only have come about after the concept of division, which he dates to after 10,000 BC, with prime numbers probably not being understood until about 500 BC. He also writes that "no attempt has been made to explain why a tally of something should exhibit multiples of two, prime numbers between 10 and 20, and some numbers that are almost multiples of 10."[17]
Predynastic Egyptians of the 5th millennium BC pictorially represented geometric designs. It has been claimed that megalithic monuments in England and Scotland, dating from the 3rd millennium BC, incorporate geometric ideas such as circles, ellipses, and Pythagorean triples in their design.[18]
All of the above are disputed however, and the currently oldest undisputed mathematical usage is in Babylonian and dynastic Egyptian sources. Thus it took human beings at least 45,000 years from the attainment of behavioral modernity and language (generally thought to be a long time before that) to develop mathematics as such.
In contrast to the sparsity of sources in Egyptian mathematics, our knowledge of Babylonian mathematics is derived from more than 400 clay tablets unearthed since the 1850s.[20] Written in Cuneiform script, tablets were inscribed whilst the clay was moist, and baked hard in an oven or by the heat of the sun. Some of these appear to be graded homework.
The earliest evidence of written mathematics dates back to the ancient Sumerians, who built the earliest civilization in Mesopotamia. They developed a complex system of metrology from 3000 BC. From around 2500 BC onwards, the Sumerians wrote multiplication tables on clay tablets and dealt with geometrical exercises and division problems. The earliest traces of the Babylonian numerals also date back to this period.[21]
The majority of recovered clay tablets date from 1800 to 1600 BC, and cover topics which include fractions, algebra, quadratic and cubic equations, and the calculation of regular reciprocal pairs.[22] The tablets also include multiplication tables and methods for solving linear and quadratic equations. The Babylonian tablet YBC 7289 gives an approximation of √2 accurate to five decimal places.
Babylonian mathematics were written using a sexagesimal (base-60) numeral system. From this derives the modern day usage of 60 seconds in a minute, 60 minutes in an hour, and 360 (60 x 6) degrees in a circle, as well as the use of seconds and minutes of arc to denote fractions of a degree. Babylonian advances in mathematics were facilitated by the fact that 60 has many divisors. Also, unlike the Egyptians, Greeks, and Romans, the Babylonians had a true place-value system, where digits written in the left column represented larger values, much as in the decimal system. They lacked, however, an equivalent of the decimal point, and so the place value of a symbol often had to be inferred from the context.
 Egyptian mathematics refers to mathematics written in the Egyptian language. From the Hellenistic period, Greek replaced Egyptian as the written language of Egyptian scholars. Mathematical study in Egypt later continued under the Arab Empire as part of Islamic mathematics, when Arabic became the written language of Egyptian scholars.
Egyptian mathematics refers to mathematics written in the Egyptian language. From the Hellenistic period, Greek replaced Egyptian as the written language of Egyptian scholars. Mathematical study in Egypt later continued under the Arab Empire as part of Islamic mathematics, when Arabic became the written language of Egyptian scholars.
The most extensive Egyptian mathematical text is the Rhind papyrus (sometimes also called the Ahmes Papyrus after its author), dated to c. 1650 BC but likely a copy of an older document from the Middle Kingdom of about 2000-1800 BC.[23] It is an instruction manual for students in arithmetic and geometry. In addition to giving area formulas and methods for multiplication, division and working with unit fractions, it also contains evidence of other mathematical knowledge,[24] including composite and prime numbers; arithmetic, geometric and harmonic means; and simplistic understandings of both the Sieve of Eratosthenes and perfect number theory (namely, that of the number 6).[25] It also shows how to solve first order linear equations[26] as well as arithmetic and geometric series.[27]
Another significant Egyptian mathematical text is the Moscow papyrus, also from the Middle Kingdom period, dated to c. 1890 BC.[28] It consists of what are today called word problems or story problems, which were apparently intended as entertainment. One problem is considered to be of particular importance because it gives a method for finding the volume of a frustum: "If you are told: A truncated pyramid of 6 for the vertical height by 4 on the base by 2 on the top. You are to square this 4, result 16. You are to double 4, result 8. You are to square 2, result 4. You are to add the 16, the 8, and the 4, result 28. You are to take one third of 6, result 2. You are to take 28 twice, result 56. See, it is 56. You will find it right."
Finally, the Berlin papyrus (c. 1300 BC[29]) shows that ancient Egyptians could solve a second-order algebraic equation.[30]
 Greek mathematics refers to the mathematics written in the Greek language from the time of Thales of Miletus (~600 BC) to the closure of the Academy of Athens in 529 AD.[31] Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to North Africa, but were united by culture and language. Greek mathematics of the period following Alexander the Great is sometimes called Hellenistic mathematics.[32]
Greek mathematics refers to the mathematics written in the Greek language from the time of Thales of Miletus (~600 BC) to the closure of the Academy of Athens in 529 AD.[31] Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to North Africa, but were united by culture and language. Greek mathematics of the period following Alexander the Great is sometimes called Hellenistic mathematics.[32]
Greek mathematics was much more sophisticated than the mathematics that had been developed by earlier cultures. All surviving records of pre-Greek mathematics show the use of inductive reasoning, that is, repeated observations used to establish rules of thumb. Greek mathematicians, by contrast, used deductive reasoning. The Greeks used logic to derive conclusions from definitions and axioms, and used mathematical rigor to prove them.[33]
Greek mathematics is thought to have begun with Thales of Miletus (c. 624–c.546 BC) and Pythagoras of Samos (c. 582–c. 507 BC). Although the extent of the influence is disputed, they were probably inspired by Egyptian and Babylonian mathematics. According to legend, Pythagoras traveled to Egypt to learn mathematics, geometry, and astronomy from Egyptian priests.
 Thales used geometry to solve problems such as calculating the height of pyramids and the distance of ships from the shore. He is credited with the first use of deductive reasoning applied to geometry, by deriving four corollaries to Thales' Theorem. As a result, he has been hailed as the first true mathematician and the first known individual to whom a mathematical discovery has been attributed.[35] Pythagoras established the Pythagorean School, whose doctrine it was that mathematics ruled the universe and whose motto was "All is number".[36] It was the Pythagoreans who coined the term "mathematics", and with whom the study of mathematics for its own sake begins. The Pythagoreans are credited with the first proof of the Pythagorean theorem,[37] though the statement of the theorem has a long history, and with the proof of the existence of irrational numbers.[38][39]
Thales used geometry to solve problems such as calculating the height of pyramids and the distance of ships from the shore. He is credited with the first use of deductive reasoning applied to geometry, by deriving four corollaries to Thales' Theorem. As a result, he has been hailed as the first true mathematician and the first known individual to whom a mathematical discovery has been attributed.[35] Pythagoras established the Pythagorean School, whose doctrine it was that mathematics ruled the universe and whose motto was "All is number".[36] It was the Pythagoreans who coined the term "mathematics", and with whom the study of mathematics for its own sake begins. The Pythagoreans are credited with the first proof of the Pythagorean theorem,[37] though the statement of the theorem has a long history, and with the proof of the existence of irrational numbers.[38][39]
Plato (428/427 BC – 348/347 BC) is important in the history of mathematics for inspiring and guiding others.[40] His Platonic Academy, in Athens, became the mathematical center of the world in the 4th century BC, and it was from this school that the leading mathematicians of the day, such as Eudoxus of Cnidus, came from.[41] Plato also discussed the foundations of mathematics, clarified some of the definitions (e.g. that of a line as "breadthless length"), and reorganized the assumptions.[42] The analytic method is ascribed to Plato, while a formula for obtaining Pythagorean triples bears his name.[41]
Eudoxus (408–c.355 BC) developed the method of exhaustion, a precursor of modern integration[43] and a theory of ratios that avoided the problem of incommensurable magnitudes.[44] The former allowed the calculations of areas and volumes of curvilinear figures,[45] while the latter enabled subsequent geometers to make significant advances in geometry. Though he made no specific technical mathematical discoveries, Aristotle (384—c.322 BC) contributed significantly to the development of mathematics by laying the foundations of logic.[46]
In the 3rd century BC, the premier center of mathematical education and research was the Musaeum of Alexandria.[47] It was there that Euclid (c. 300 BC) taught, and wrote the Elements, widely considered the most successful and influential textbook of all time.[1] The Elements introduced mathematical rigor through the axiomatic method and is the earliest example of the format still used in mathematics today, that of definition, axiom, theorem, and proof. Although most of the contents of the Elements were already known, Euclid arranged them into a single, coherent logical framework.[48] The Elements was known to all educated people in the West until the middle of the 20th century and its contents are still taught in geometry classes today.[49] In addition to the familiar theorems of Euclidean geometry, the Elements was meant as an introductory textbook to all mathematical subjects of the time, such as number theory, algebra and solid geometry,[48] including proofs that the square root of two is irrational and that there are infinitely many prime numbers. Euclid also wrote extensively on other subjects, such as conic sections, optics, spherical geometry, and mechanics, but only half of his writings survive.[50]
Archimedes (c.287–212 BC) of Syracuse, widely considered the greatest mathematician of antiquity,[51] used the method of exhaustion to calculate the area under the arc of a parabola with the summation of an infinite series, in a manner not too dissimilar from modern calculus.[52] He also showed one could use the method of exhaustion to calculate the value of π with as much precision as desired, and obtained the most accurate value of π then known, 310⁄71 < π < 310⁄70.[53] He also studied the spiral bearing his name, obtained formulas for the volumes of surfaces of revolution (paraboloid, ellipsoid, hyperboloid),[52] and an ingenious system for expressing very large numbers.[54] While he is also known for his contributions to physics and several advanced mechanical devices, Archimedes himself placed far greater value on the products of his thought and general mathematical principles.[55] He regarded as his greatest achievement his finding of the surface area and volume of a sphere, which he obtained by proving these are 2/3 the surface area and volume a cylinder circumscribing the sphere.[56]
Apollonius of Perga (c. 262-190 BC) made significant advances to the study of conic sections, showing that one can obtain all three varieties of conic section by varying the angle of the plane that cuts a double-napped cone.[57] He also coined the terminology in use today for conic sections, namely parabola ("place beside" or "comparison"), "ellipse" ("deficiency"), and "hyperbola" ("a throw beyond").[58] His work Conics is one of the best known and preserved mathematical works from antiquity, and in it he derives many theorems concerning conic sections that would prove invaluable to later mathematicians and astronomers studying planetary motion, such as Isaac Newton.[59] While neither Apollonius nor any other Greek mathematicians made the leap to coordinate geometry, Apollonius' treatment of curves is in some ways similar to the modern treatment, and some of his work seems to anticipate the development of analytical geometry by Descartes some 1800 years later.[60]
Around the same time, Eratosthenes of Cyrene of Cyrene (c. 276-194 BC) devised the Sieve of Eratosthenes for finding prime numbers.[61] The 3rd century BC is generally regarded as the "Golden Age" of Greek mathematics, with advances in pure mathematics henceforth in relative decline.[62] Nevertheless, in the centuries that followed significant advances were made in applied mathematics, most notably trigonometry, largely to address the needs of astronomers.[63] Hipparchus of Nicaea (c. 190-120 BC) is considered the founder of trigonometry for compiling the first known trigonometric table, and to him is also due the systematic use of the 360 degree circle.[64] Heron of Alexandria (c. 10–70 AD) is credited with Heron's formula for finding the area of a scalene triangle and with being the first to recognize the possibility of negative numbers possessing square roots.[65] Menelaus of Alexandria (c. 100 AD) pioneered spherical trigonometry through Menelaus' theorem.[66] The most complete and influential trigonometric work of antiquity is the Almagest of Ptolemy (c. AD 90-168), a landmark astronomical treatise whose trigonometric tables would be used by astronomers for the next thousand years.[67] Ptolemy is also credited with Ptolemy's theorem for deriving trigonometric quantities, and the most accurate value of π outside of China until the medieval period, 3.1416.[68]
Following a period of stagnation after Ptolemy, the period between 250 and 350 AD is sometimes referred to as the "Silver Age" of Greek mathematics.[69] During this period, Diophantus made significant advances in algebra, particularly indeterminate analysis, which is also known as "Diophantine analysis".[70] The study of Diophantine equations and Diophantine approximations is a significant area of research to this day. His main work was the Arithmetica, a collection of 150 algebraic problems dealing with exact solutions to determinate and indeterminate equations.[71] The Arithmetica had a significant influence on later mathematicians, such as Pierre de Fermat, who arrived at his famous Last Theorem after trying to generalize a problem he had read in the Arithmetica (that of dividing a square into two squares).[72] Diophantus also made significant advances in notation, the Arithmetica being the first instance of algebraic symbolism and syncopation.[73]
BY PROF JACOB
The area of study known as the history of mathematics is primarily an investigation into the origin of discoveries in mathematics and, to a lesser extent, an investigation into the mathematical methods and notation of the past.
Before the modern age and the worldwide spread of knowledge, written examples of new mathematical developments have come to light only in a few locales. The most ancient mathematical texts available are Plimpton 322 (Babylonian mathematics c. 1900 BC),[2] the Rhind Mathematical Papyrus (Egyptian mathematics c. 2000-1800 BC)[3] and the Moscow Mathematical Papyrus (Egyptian mathematics c. 1890 BC). All of these texts concern the so-called Pythagorean theorem, which seems to be the most ancient and widespread mathematical development after basic arithmetic and geometry.
The study of mathematics as a subject in its own right begins in the 6th century BC with the Pythagoreans, who coined the term "mathematics" from the ancient Greek μάθημα (mathema), meaning "subject of instruction".[4] Greek mathematics greatly refined the methods (especially through the introduction of deductive reasoning and mathematical rigor in proofs) and expanded the subject matter of mathematics.[5] Chinese mathematics made early contributions, including a place value system.[6][7] The Hindu-Arabic numeral system and the rules for the use of its operations, in use throughout the world today, likely evolved over the course of the first millennium AD in India and was transmitted to the west via Islamic mathematics.[8][9] Islamic mathematics, in turn, developed and expanded the mathematics known to these civilizations.[10] Many Greek and Arabic texts on mathematics were then translated into Latin, which led to further development of mathematics in medieval Europe.
From ancient times through the Middle Ages, bursts of mathematical creativity were often followed by centuries of stagnation. Beginning in Renaissance Italy in the 16th century, new mathematical developments, interacting with new scientific discoveries, were made at an increasing pace that continues through the present day.
| |
[edit] Prehistoric mathematics
The origins of mathematical thought lie in the concepts of number, magnitude, and form.[11] Modern studies of animal cognition have shown that these concepts are not unique to humans. Such concepts would have been part of everyday life in hunter-gatherer societies. The idea of the "number" concept evolving gradually over time is supported by the existence of languages which preserve the distinction between "one", "two", and "many", but not of numbers larger than two.[11]The oldest known possibly mathematical object is the Lebombo bone, discovered in the Lebombo mountains of Swaziland and dated to approximately 35,000 BC.[12] It consists of 29 distinct notches cut into a baboon's fibula.[13] Also prehistoric artifacts discovered in Africa and France, dated between 35,000 and 20,000 years old,[14] suggest early attempts to quantify time.[15]
The Ishango bone, found near the headwaters of the Nile river (northeastern Congo), may be as much as 20,000 years old and consists of a series of tally marks carved in three columns running the length of the bone. Common interpretations are that the Ishango bone shows either the earliest known demonstration of sequences of prime numbers[13] or a six month lunar calendar.[16] In the book How Mathematics Happened: The First 50,000 Years, Peter Rudman argues that the development of the concept of prime numbers could only have come about after the concept of division, which he dates to after 10,000 BC, with prime numbers probably not being understood until about 500 BC. He also writes that "no attempt has been made to explain why a tally of something should exhibit multiples of two, prime numbers between 10 and 20, and some numbers that are almost multiples of 10."[17]
Predynastic Egyptians of the 5th millennium BC pictorially represented geometric designs. It has been claimed that megalithic monuments in England and Scotland, dating from the 3rd millennium BC, incorporate geometric ideas such as circles, ellipses, and Pythagorean triples in their design.[18]
All of the above are disputed however, and the currently oldest undisputed mathematical usage is in Babylonian and dynastic Egyptian sources. Thus it took human beings at least 45,000 years from the attainment of behavioral modernity and language (generally thought to be a long time before that) to develop mathematics as such.
[edit] Babylonian mathematics
Main article: Babylonian mathematics
See also: Plimpton 322
Babylonian mathematics refers to any mathematics of the people of Mesopotamia (modern Iraq) from the days of the early Sumerians through the Hellenistic period almost to the dawn of Christianity.[19] It is named Babylonian mathematics due to the central role of Babylon as a place of study. Later under the Arab Empire, Mesopotamia, especially Baghdad, once again became an important center of study for Islamic mathematics.In contrast to the sparsity of sources in Egyptian mathematics, our knowledge of Babylonian mathematics is derived from more than 400 clay tablets unearthed since the 1850s.[20] Written in Cuneiform script, tablets were inscribed whilst the clay was moist, and baked hard in an oven or by the heat of the sun. Some of these appear to be graded homework.
The earliest evidence of written mathematics dates back to the ancient Sumerians, who built the earliest civilization in Mesopotamia. They developed a complex system of metrology from 3000 BC. From around 2500 BC onwards, the Sumerians wrote multiplication tables on clay tablets and dealt with geometrical exercises and division problems. The earliest traces of the Babylonian numerals also date back to this period.[21]
The majority of recovered clay tablets date from 1800 to 1600 BC, and cover topics which include fractions, algebra, quadratic and cubic equations, and the calculation of regular reciprocal pairs.[22] The tablets also include multiplication tables and methods for solving linear and quadratic equations. The Babylonian tablet YBC 7289 gives an approximation of √2 accurate to five decimal places.
Babylonian mathematics were written using a sexagesimal (base-60) numeral system. From this derives the modern day usage of 60 seconds in a minute, 60 minutes in an hour, and 360 (60 x 6) degrees in a circle, as well as the use of seconds and minutes of arc to denote fractions of a degree. Babylonian advances in mathematics were facilitated by the fact that 60 has many divisors. Also, unlike the Egyptians, Greeks, and Romans, the Babylonians had a true place-value system, where digits written in the left column represented larger values, much as in the decimal system. They lacked, however, an equivalent of the decimal point, and so the place value of a symbol often had to be inferred from the context.
[edit] Egyptian mathematics
Main article: Egyptian mathematics

Image of Problem 14 from the Moscow Mathematical Papyrus. The problem includes a diagram indicating the dimensions of the truncated pyramid.
The most extensive Egyptian mathematical text is the Rhind papyrus (sometimes also called the Ahmes Papyrus after its author), dated to c. 1650 BC but likely a copy of an older document from the Middle Kingdom of about 2000-1800 BC.[23] It is an instruction manual for students in arithmetic and geometry. In addition to giving area formulas and methods for multiplication, division and working with unit fractions, it also contains evidence of other mathematical knowledge,[24] including composite and prime numbers; arithmetic, geometric and harmonic means; and simplistic understandings of both the Sieve of Eratosthenes and perfect number theory (namely, that of the number 6).[25] It also shows how to solve first order linear equations[26] as well as arithmetic and geometric series.[27]
Another significant Egyptian mathematical text is the Moscow papyrus, also from the Middle Kingdom period, dated to c. 1890 BC.[28] It consists of what are today called word problems or story problems, which were apparently intended as entertainment. One problem is considered to be of particular importance because it gives a method for finding the volume of a frustum: "If you are told: A truncated pyramid of 6 for the vertical height by 4 on the base by 2 on the top. You are to square this 4, result 16. You are to double 4, result 8. You are to square 2, result 4. You are to add the 16, the 8, and the 4, result 28. You are to take one third of 6, result 2. You are to take 28 twice, result 56. See, it is 56. You will find it right."
Finally, the Berlin papyrus (c. 1300 BC[29]) shows that ancient Egyptians could solve a second-order algebraic equation.[30]
[edit] Greek mathematics
Main article: Greek mathematics

The Pythagorean theorem. The Pythagoreans are generally credited with the first proof of the theorem.
Greek mathematics was much more sophisticated than the mathematics that had been developed by earlier cultures. All surviving records of pre-Greek mathematics show the use of inductive reasoning, that is, repeated observations used to establish rules of thumb. Greek mathematicians, by contrast, used deductive reasoning. The Greeks used logic to derive conclusions from definitions and axioms, and used mathematical rigor to prove them.[33]
Greek mathematics is thought to have begun with Thales of Miletus (c. 624–c.546 BC) and Pythagoras of Samos (c. 582–c. 507 BC). Although the extent of the influence is disputed, they were probably inspired by Egyptian and Babylonian mathematics. According to legend, Pythagoras traveled to Egypt to learn mathematics, geometry, and astronomy from Egyptian priests.

One of the oldest surviving fragments of Euclid's Elements, found at Oxyrhynchus and dated to circa AD 100. The diagram accompanies Book II, Proposition 5.[34]
Plato (428/427 BC – 348/347 BC) is important in the history of mathematics for inspiring and guiding others.[40] His Platonic Academy, in Athens, became the mathematical center of the world in the 4th century BC, and it was from this school that the leading mathematicians of the day, such as Eudoxus of Cnidus, came from.[41] Plato also discussed the foundations of mathematics, clarified some of the definitions (e.g. that of a line as "breadthless length"), and reorganized the assumptions.[42] The analytic method is ascribed to Plato, while a formula for obtaining Pythagorean triples bears his name.[41]
Eudoxus (408–c.355 BC) developed the method of exhaustion, a precursor of modern integration[43] and a theory of ratios that avoided the problem of incommensurable magnitudes.[44] The former allowed the calculations of areas and volumes of curvilinear figures,[45] while the latter enabled subsequent geometers to make significant advances in geometry. Though he made no specific technical mathematical discoveries, Aristotle (384—c.322 BC) contributed significantly to the development of mathematics by laying the foundations of logic.[46]
In the 3rd century BC, the premier center of mathematical education and research was the Musaeum of Alexandria.[47] It was there that Euclid (c. 300 BC) taught, and wrote the Elements, widely considered the most successful and influential textbook of all time.[1] The Elements introduced mathematical rigor through the axiomatic method and is the earliest example of the format still used in mathematics today, that of definition, axiom, theorem, and proof. Although most of the contents of the Elements were already known, Euclid arranged them into a single, coherent logical framework.[48] The Elements was known to all educated people in the West until the middle of the 20th century and its contents are still taught in geometry classes today.[49] In addition to the familiar theorems of Euclidean geometry, the Elements was meant as an introductory textbook to all mathematical subjects of the time, such as number theory, algebra and solid geometry,[48] including proofs that the square root of two is irrational and that there are infinitely many prime numbers. Euclid also wrote extensively on other subjects, such as conic sections, optics, spherical geometry, and mechanics, but only half of his writings survive.[50]
Archimedes (c.287–212 BC) of Syracuse, widely considered the greatest mathematician of antiquity,[51] used the method of exhaustion to calculate the area under the arc of a parabola with the summation of an infinite series, in a manner not too dissimilar from modern calculus.[52] He also showed one could use the method of exhaustion to calculate the value of π with as much precision as desired, and obtained the most accurate value of π then known, 310⁄71 < π < 310⁄70.[53] He also studied the spiral bearing his name, obtained formulas for the volumes of surfaces of revolution (paraboloid, ellipsoid, hyperboloid),[52] and an ingenious system for expressing very large numbers.[54] While he is also known for his contributions to physics and several advanced mechanical devices, Archimedes himself placed far greater value on the products of his thought and general mathematical principles.[55] He regarded as his greatest achievement his finding of the surface area and volume of a sphere, which he obtained by proving these are 2/3 the surface area and volume a cylinder circumscribing the sphere.[56]
Apollonius of Perga (c. 262-190 BC) made significant advances to the study of conic sections, showing that one can obtain all three varieties of conic section by varying the angle of the plane that cuts a double-napped cone.[57] He also coined the terminology in use today for conic sections, namely parabola ("place beside" or "comparison"), "ellipse" ("deficiency"), and "hyperbola" ("a throw beyond").[58] His work Conics is one of the best known and preserved mathematical works from antiquity, and in it he derives many theorems concerning conic sections that would prove invaluable to later mathematicians and astronomers studying planetary motion, such as Isaac Newton.[59] While neither Apollonius nor any other Greek mathematicians made the leap to coordinate geometry, Apollonius' treatment of curves is in some ways similar to the modern treatment, and some of his work seems to anticipate the development of analytical geometry by Descartes some 1800 years later.[60]
Around the same time, Eratosthenes of Cyrene of Cyrene (c. 276-194 BC) devised the Sieve of Eratosthenes for finding prime numbers.[61] The 3rd century BC is generally regarded as the "Golden Age" of Greek mathematics, with advances in pure mathematics henceforth in relative decline.[62] Nevertheless, in the centuries that followed significant advances were made in applied mathematics, most notably trigonometry, largely to address the needs of astronomers.[63] Hipparchus of Nicaea (c. 190-120 BC) is considered the founder of trigonometry for compiling the first known trigonometric table, and to him is also due the systematic use of the 360 degree circle.[64] Heron of Alexandria (c. 10–70 AD) is credited with Heron's formula for finding the area of a scalene triangle and with being the first to recognize the possibility of negative numbers possessing square roots.[65] Menelaus of Alexandria (c. 100 AD) pioneered spherical trigonometry through Menelaus' theorem.[66] The most complete and influential trigonometric work of antiquity is the Almagest of Ptolemy (c. AD 90-168), a landmark astronomical treatise whose trigonometric tables would be used by astronomers for the next thousand years.[67] Ptolemy is also credited with Ptolemy's theorem for deriving trigonometric quantities, and the most accurate value of π outside of China until the medieval period, 3.1416.[68]
Following a period of stagnation after Ptolemy, the period between 250 and 350 AD is sometimes referred to as the "Silver Age" of Greek mathematics.[69] During this period, Diophantus made significant advances in algebra, particularly indeterminate analysis, which is also known as "Diophantine analysis".[70] The study of Diophantine equations and Diophantine approximations is a significant area of research to this day. His main work was the Arithmetica, a collection of 150 algebraic problems dealing with exact solutions to determinate and indeterminate equations.[71] The Arithmetica had a significant influence on later mathematicians, such as Pierre de Fermat, who arrived at his famous Last Theorem after trying to generalize a problem he had read in the Arithmetica (that of dividing a square into two squares).[72] Diophantus also made significant advances in notation, the Arithmetica being the first instance of algebraic symbolism and syncopation.[73]
Subscribe to:
Posts (Atom)